Итерации и свойства фракталов.
Iteration - повторение [одного и того же действия] (англ.)
В общем случае рассматриваются нелинейные процессы в n-мерных пространствах. Наиболее просты в изучении двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоватся терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние ( или как говорят - аттрактор ) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы ( итерационного процесса ). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами.
Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
 |
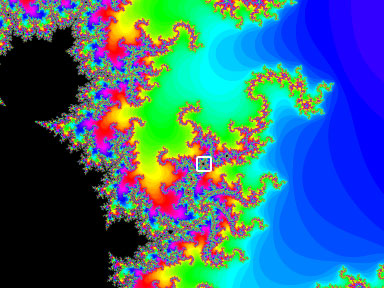 |
| Рис 1. Множество Мандельброта. По горизонтальной оси варьируются действительные значения Cx, а по вертикальной оси мнимые значения Cy. | Рис 2. Участок границы множества Мандельброта, ( на рис.1 выделенный белым квадратом ) увеличенный в 17 раз. |
В качестве примера рассмотрим множество Мандельброта ( см. рис.1 ). Алгоритм его построения достаточно прост и основан на простом итерационном процессе:
Z[1] = Z[0] * Z[0] + C,
Z[2] = Z[1] * Z[1] + C,
. . .
Z[i+1] = Z[i] * Z[i] + C,
. . .
где Z[i] и С - комплексные переменные. Итерации выполняются для каждой стартовой точки С прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), ( это означает, что аттрактор динамической системы находится в бесконечности ), или после достаточно большого числа итераций ( например 200-500 ) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки С ( если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет ).
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность ( точки имеющие черный цвет ). Точки принадлежащие границе множества ( именно там возникает сложные структуры ) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций ( красный фон ).
 |
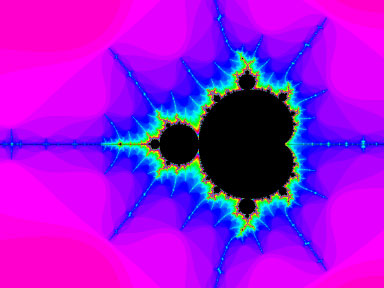 |
| Рис 3. Участок множества Мандельброта, ( на рис.2 выделенный белым квадратом ) увеличенный в 13 раз. | Рис 4. Участок множества Мандельброта, симметричный относительно действительной оси координат, ( на рис.1 выделенный зеленым квадратом ) точно подобный всему фракталу. |
Рис.3 демонстрирует приблизительное подобие участка границы фрактала всему фракталу (при повороте на ~108 градусов против часовой стрелки). Из рисунков 3 и 4 видно, что итерационный процесс Z[i+1] = Z[i] * Z[i] + C порождает подобие отдельных участков и самоподобие фрактала в целом.
Даже если мы увеличиваем изображение в миллиарды (!) раз, как показано на этом видео, все равно находится участок (на этот раз при повороте на ~ 90 градусов по часовой стрелке) подобный всему фракталу в целом. (комментарий Адриена Дуади, фр.)
Множества Жюлиа.
Как поведут себя итерации Z(n) при различных начальных условиях Z(0). При каких Z(0) итерации Z(n) ограничены?
Множество начальных значений Z(0), при которых итерации Z(n) ограничены (при заданном значении параметра C), образуют так называемое заполненное множество Жюлиа Jc. (Собственно множеством Жюлиа называется множество граничных точек множества Jc.) Как показал компьютерный эксперимент, различные значения параметра C могут порождать поразительно разнообразные множества Жюлиа, причем малейшие изменения параметра C нередко приводят к весьма существенным метаморфозам множеств Jc

Некоторые множества Жюлиа связны, другие представляют собой «пылевидные» канторовы множества (Как видно из представленного выше рисунка, красными стрелками указано откуда берутся значения параметра C для построения соответствующего множества Жюлия, если параметр C не принадлежит множеству Мандельброта множество Жюлия "пылевидно", тоесть не связно). Интересно, что абсолютно все значения параметра C, при которых Jc связны, принадлежат М-множеству, поэтому последнее может быть определено и как множество всех значений параметра C, при которых Jc — связно. Эта эквивалентность следует из теоремы, доказанной независимо друг от друга Гастоном Жюлиа и Пьером Фату в 1918 г. и переоткрытой в совместной работе Дуади и Хаббарда, которые существенно расширили наши все еще отрывочные знания об обманчиво простом отображении Z[i+1] = Z[i] * Z[i] + C.

Одно из наиболее важных открытий Дуади и Хаббарда состоит в том, что граница множества Мандельброта может быть конформно отображена на единичную окружность, и что итерации Z(n+1) = Z(n)*Z(n) + C соответствуют простому удвоению угла на единичной окружности. Таким образом, если измерять углы а в величинах кратных 2пи, то комплексное квадратичное отображение соответствует отображению a(n+1) = = 2а(n) mod 1. Если «внешний угол» а, как его принято называть, выразить в виде двоичной дроби, то такое отображение соответствует сдвигу двоичных цифр влево по модулю 1.
Например, значение параметра с внешним углом а в 13/31 = 0, (11011) приводит к периодической орбите с длиной периода 5. Конкретные цифры указывают, какая из итераций Z(n) попадет в верхнюю (0), а какая — в нижнюю (1) полуплоскость. На нижнем рисунке изображено М-множество и указаны некоторые рациональные внешние углы. Точка сгущения бифуркаций удвоения периода C = —1,4011... (она отмечена буквой QF в честь Фейгенбаума) имеет в качестве своего внешнего угла постоянную Морса-Туэ 0,0110100110010110... = 0,412..., двоичные цифры которой образуют последовательность Морса-Туэ.
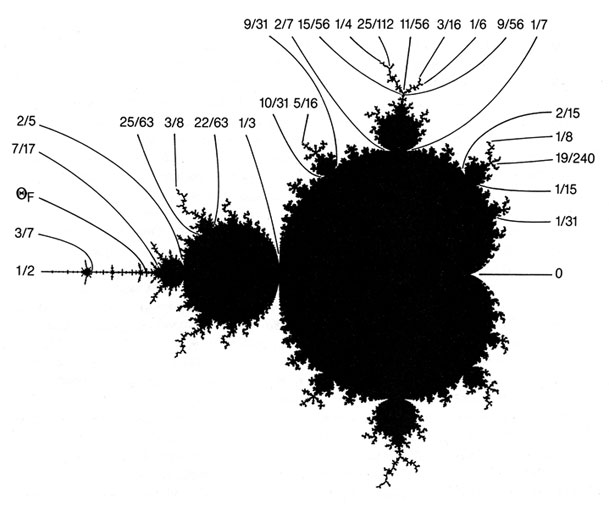
Конформному отображению границы М-множества на единичную окружность можно придать наглядный физический смысл, если его интерпретировать как задачу электростатики. Рассмотрим бесконечно длинный проводящий стержень, поперечное сечение которого совпадает с М-множеством, окружим его на большом удалении электродом в форме кругового цилиндра и создадим между стержнем и цилиндром разность потенциалов. Тогда силовые линии электрического поля, выходящие из точки на единичной окружности, проведенный через которую радиус образует с вещественной осью угол а, заканчиваются в точке C с внешним углом а на границе М-множества. Так происходит потому, что силовые линии электрического поля подчиняются законам конформного отображения. А эквипотенциальные линии, ортогональные к силовым линиям, соответствуют значениям C с равными скоростями расходимости итераций Z(n) в бесконечность при Z(0) = 0.
( Напомним, что лежащие вне М-множества значения параметра C приводят к неограниченным итерациям Z(n). )
Из книги Пайтген Х. О., Рихтер П. Х. "Красота фракталов".
Еще одно свойство фракталов, проявляющееся при изменении масштаба.
Как видно из просмотра этого видео при изменении масштаба фрактал проявляет новые структуры наряду с повторяющимся основным узором, при этом не иссякает информационный поток от изображения. Этим свойством также обладают физические объекты, как это наиболее очевидно, когда мы рассматриваем масштабируемое изображение со спутника.