Magnetic field of the coil with a current.

Calculation of an optimum ratio of the diameter to the lenght of the coil.

 

 

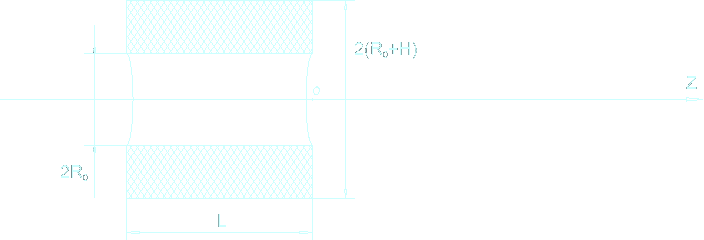
The task consists in finding such L and H at which a magnetic field on an axis z, at a point Z = 0, would be maximum, at other identical parametres.
Formula for the magnetic field on Z axis of coil with a current looks so:

 

 

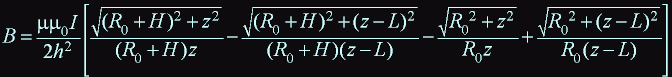
where h - is thikness of a wire, resistance of the wire:

 

 

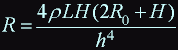
length of wire:

 

 

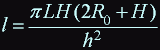
current:

 

       

 

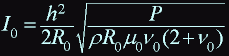
here P - is dissipated power, field at a point z = 0:

 

 

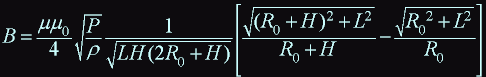
having entered dimensionless parameters , we have:

 

 

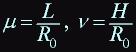
then the formula for a magnetic field at a point z = 0 takes form:

 

 

 

 

 

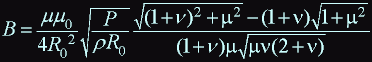
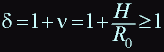
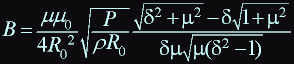
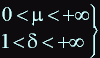
Let:

 

 

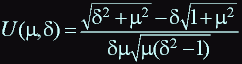
- dimensionless function of two parametres which has a maximum, according to a reasoning:

 

 

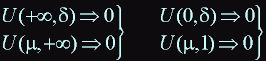
from this it follows that there exist optimal values :

 

 

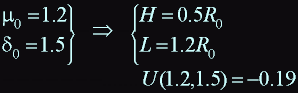
Thus we have found that at L = 1.2 R0, and H = 0.5 R0 a magnetic field at the centre of coil maximum.

 

 

 

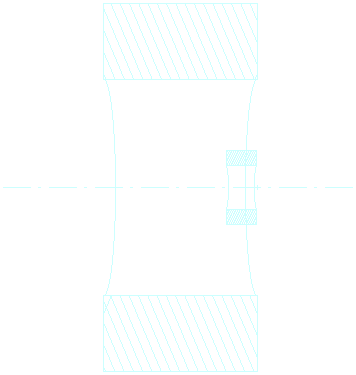
The figure shows two coils of different sizes, but have equal proportions with the optimum ratio of coil length to height of the wound wire.

© 1992 - 2024 Alexander Kucherenko