5.2. Задача Элитцура — Вайдмана об испытании бомб

Вообразим себе бомбу, в носовой части которой закреплен детонатор, настолько чувствительный, что при малейшем давлении на него бомба взрывается. Для срабатывания такого детонатора достаточно одного-единственного фотона видимого света, хотя в некоторых случаях детонатор заклинивает, и бомба взорваться не может — бомбу с неисправным детонатором мы будем называть «холостой». Предположим, что детонатор снабжен зеркальцем, подвижно закрепленным на носу бомбы таким образом, что при отражении зеркальцем одного фотона (видимого света) оно смещается и приводит в движение ударный механизм, в результате чего бомба взрывается — за исключением, разумеется, тех случаев, когда бомба оказывается холостой, т. е. когда чувствительный механизм детонатора заклинивает. Поскольку все упомянутые устройства работают по классическим законам, мы должны также предположить, что после того, как бомба собрана, выяснить, не заклинило ли ее детонатор, невозможно без того, чтобы этот самый детонатор так или иначе не потревожить — что непременно приведет к немедленному взрыву. ( Необходимо ввести еще одно допущение: детонатор может заклинить только в процессе сборки, по завершении сборки детонатор либо исправен, либо нет; ( см. рис. 5.1. ) 

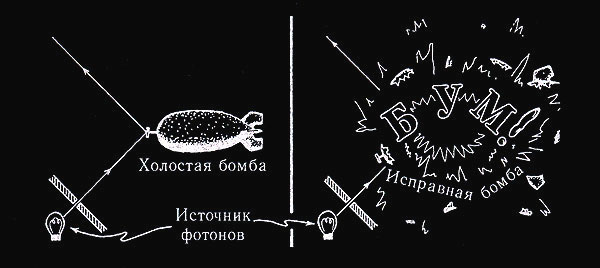
Рис. 5.1. Задача Элитцура —Вайдмана об испытании бомб. Сверхчувствительный детонатор бомбы срабатывает от соприкосновения с одним-единственным оптическим фотоном — может, впрочем, и не сработать, если его заклинит, в каковом случае бомба считается холостой. Задача: найти гарантированно исправную бомбу при наличии большого количества бомб сомнительного качества.

Допустим, что таких бомб у нас огромное количество ( денег мы здесь не считаем! ), однако доля холостых среди них может оказаться чрезмерно высокой. Задача заключается в том, чтобы найти хотя бы одну бомбу, о которой можно было бы заранее с уверенностью сказать: «Вот эта точно сработает».

Эта задача ( вместе с решением ) была предложена Авшаломом Элитцуром и Львом Вайдманом. Я не буду приводить решение прямо здесь, так как, возможно, кто-то из читателей, уже знакомых с квантовой теорией и с теми занимательными головоломками, которые я определил выше как Z-загадки, пожелает попробовать свои силы ( интеллектуальные, разумеется ) в отыскании этого самого решения. Достаточно будет сказать, что решение существует и даже, при неограниченном запасе бомб такого рода, не выходит за рамки современных технических возможностей. Тех же, кто в квантовой теории пока не сведущ ( либо просто не склонен тратить время на поиски решения ), я прошу потерпеть еще некоторое время ( или, если хотите, можете сразу заглянуть в §5.9 ). Всему свое время — сначала я попытаюсь объяснить некоторые фундаментальные квантовые идеи, а затем приведу решение.

На данном этапе рассуждения необходимо лишь отметить: одно то, что эта задача имеет-таки решение ( квантовомеханическое ), уже указывает на глубинное различие между квантовой и классической физикой. При классическом подходе выяснить, не заклинило ли детонатор бомбы, можно только посредством приложения к нему какого-либо реального физического усилия ( при этом, если детонатор исправен, бомба взрывается, и эксперимент считается благополучно проваленным ). В рамках квантовой теории возможны и иные варианты — например, физический эффект, являющийся результатом того, что к детонатору могло быть приложено усилие, в то время как в действительности ничего подобного не произошло. В этом, собственно, и состоит одна из наиболее любопытных особенностей квантовой теории: реальный физический эффект здесь вполне может являться результатом контрфактуальных ( как говорят философы ) действий, т. е. действий, которые могли произойти, хотя на деле и не произошли. При рассмотрении следующей Z-загадки мы убедимся, что контрфактуальность играет далеко не последнюю роль и в ситуациях иного рода.

...

5.9. Решение задачи Элитцура — Вайдмана об испытании бомб

Мы уже знаем вполне достаточно для того, чтобы отыскать решение задачи об испытании бомб, поставленной в §5.2. Прежде всего нужно выяснить, нельзя ли использовать сверхчувствительное зеркальце на носу бомбы в качестве измерительного устройства ( как были использованы, например, препятствие и подвижное зеркало с детектором в описанных выше примерах ). Построим систему зеркал ( два непрозрачных, два полупрозрачных ), которая в точности повторяет систему из предыдущего примера ( см. рис. 5.14 ) 

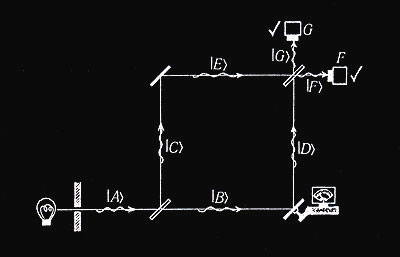
Рис. 5.14. Аналогичного эффекта можно достичь, поместив в правый нижний угол подвижное зеркало, снабженное неким детектором, который способен по движению зеркала определить, отразило оно фотон или нет. Интерференция здесь также оказывается нарушена, благодаря чему детектор в точке G получает возможность зарегистрировать прибытие фотона.

за одним исключением: в правом нижнем углу вместо подвижного зеркала поместим зеркальце бомбы. Смысл такого построения в том, что если бомба является холостой ( в том единственном смысле, который подразумевается в условии задачи ), то ее зеркальце остается в любом случае неподвижным ( поскольку его заклинило ), и общая картина эквивалентна показанной на рис. 5.12. 

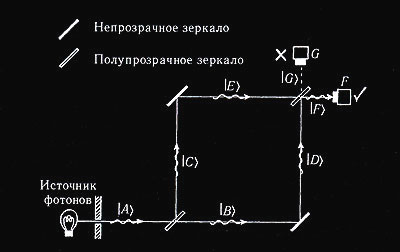
Рис. 5.12. Две составляющие состояния фотона сводятся вместе посредством двух непрозрачных зеркал; в точке слияния двух лучей установлено еще одно полупрозрачное зеркало. Лучи интерферируют таким образом, что результирующий луч приобретает состояние |F), тогда как детектор в точке G фотона не регистрирует.

Фотон, испущенный из источника, попадает на первое зеркало, будучи в состоянии |А}. Фотон после последнего зеркала приобретает состояние |F} ( пропорциональное |F}, если точнее ). Иначе говоря, детектор в точке F регистрирует прибытие фотона, а детектор в точке G не регистрирует ничего.

Если же бомба исправна, то падение фотона на ее зеркальце приводит к срабатыванию детонатора, и бомба взрывается. Бомба, фактически, представляет собой измерительное устройство. Альтернативы квантового уровня —«фотон падает на зеркальце» и «фотон не падает на зеркальце» — переводятся бомбой в альтернативы классического уровня — «бомба взрывается» и «бомба не взрывается». На состояние

|В} + i*|С}

бомба реагирует взрывом, если обнаруживает, что фотон находится в состоянии |В}; если же фотон находится в каком-то ином состоянии (т.е., в данном случае, |С}), бомба не взрывается. Отношение вероятностей этих двух событий равно

1*1 : i*i = 1:1.

Если бомба таки взорвалась, это означает, что она зарегистрировала прибытие фотона, а что будет дальше, никого уже не интересует. Если же взорваться бомбе не удалось, то состояние фотона редуцируется ( как результат процедуры R ) до состояния i*|С} ( падение на зеркало в левом верхнем углу ), сменяясь далее ( после отражения от этого зеркала ) состоянием — |Е}. По прохождении последнего ( полупрозрачного ) зеркала фотон переходит в состояние

- |F} - i*|G},

т. е. отношение вероятностей возможных исходов — «прибытие фотона регистрируется детектором в точке F» и «прибытие фотона регистрируется детектором в точке G» - равно

(-1)*(-1) : (-i)*(-i) = 1 : 1.

Точно такое же отношение мы получили в примерах, описанных в предыдущем параграфе, для тех случаев, когда фотон не поглощался препятствием, а стрелка не отклонялась. Детектор, расположенный в точке G, получает, таким образом, вполне определенную возможность уловить фотон. Предположим теперь, что при проведении одного из таких испытаний в некоторых случаях «не-взрыва» бомбы обнаруживается, что детектор G и в самом деле регистрирует прибытие фотона. Согласно нашим рассуждениям, это возможно лишь в том случае, если детонатор бомбы исправен! Если бомба неисправна, то фотон может быть зарегистрирован только детектором F. Следовательно, во всех случаях, когда срабатывает детектор G, мы можем с чистой совестью гарантировать, что данная бомба «работоспособна» и в случае необходимости не подведет. Таким образом, задачу об испытании бомб ( 5.2 ) можно считать решенной.

Судя по участвующим в процессе вероятностям, после достаточно большого количества испытаний половина бомб взорвется, и никакой дальнейшей пользы из них извлечь не удастся. Более того, на тех бомбах, что не взорвались, детектор G сработает только в половине случаев. Таким образом, после того, как мы переберем все бомбы одну за другой, мы сможем гарантировать работоспособность только четверти из первоначального запаса исправных бомб. Оставшиеся бомбы мы можем подвергнуть повторному испытанию, отбирая те, на которых сработал детектор G. Повторим испытание еще раз. И еще. В конечном счете у нас останется треть (поскольку 1/4 + 1/16 + 1/64 ... = 1/3) от первоначального количества исправных бомб, но зато все эти бомбы будут гарантированно работоспособны. ( Я не знаю, для чего эти бомбы предназначены, однако, думаю, благоразумно будет лишних вопросов не задавать! )

Читателю описанная процедура может показаться чересчур расточительной, однако поразительно здесь то, что она вообще осуществима. Никакими классическими методами задача не решается. Только в квантовой теории контрфактуальные вероятности могут действительно повлиять на физический результат. Наша квантовая процедура позволяет добиться того, что кажется невозможным, — что и в самом деле невозможно в рамках классической физики. Следует, кроме того, отметить, что с помощью некоторых усовершенствований потери можно снизить с двух третей до практически половины. Еще более поразительного результата добились не так давно П. Г. Квят, X. Вайнфуртер, А. Цайлингер и М. Казевич, описав процедуру ( отличную от решения Элитцура — Вайдмана ), позволяющую снизить потери почти до нуля!

Что касается сложностей с разработкой экспериментального устройства, способного испускать отдельные фотоны по одному за раз, то они теперь позади — такие устройства уже созданы и вполне доступны.

В заключение отмечу, что в качестве измерительного устройства вовсе не обязательно должен выступать столь «сногсшибательный» объект, как фигурирующая в условии задачи бомба. Более того, нет никакой необходимости в том, чтобы упомянутое «устройство» оповещало бы весь внешний мир о том, что оно зарегистрировало ( или не зарегистрировало ) прибытие фотона. Подвижное зеркало может само по себе послужить измерительным устройством, если его вес достаточно мал для того, чтобы оно могло сколько-нибудь заметно поворачиваться под воздействием падающих на него фотонов и затем останавливаться вследствие трения. Один лишь факт подвижности зеркала ( скажем, зеркала в правом нижнем углу, как в рассмотренном примере ) позволит детектору в точке G зарегистрировать прибытие фотона, даже если зеркало в действительности и не повернулось, указывая тем самым на то, что фотон отправился другой дорогой.

Достичь точки G фотону позволяет потенциальная возможность поворота зеркала* и ничто иное!

... Такие отрицательные и бесконтактные измерения, называемые нулевыми ( или невзаимодействующими ) измерениями, имеют большое теоретическое ( а возможно, в конечном счете, и практическое ) значение. Предсказания квантовой теории относительно такого рода ситуаций непосредственно подтверждаются экспериментально. В частности, Квят, Вайнфуртер и Цайлингер разработали и провели эксперимент, точно воспроизводящий теоретическую процедуру Элитцура —Вайдмана для решения задачи об испытании бомб! И теоретические ожидания полностью подтвердились, что, впрочем, нас уже почему-то не удивляет. Сами же нулевые измерения мы по праву относим к наиболее фундаментальным Z-загадкам квантовой теории.

Из книги: Роджер Пенроуз "Тени Разума" (в поисках науки о сознании)**

 

* - [ Прим. А. К. "потенциальная возможность поворота зеркала" относится к физической реальности или к метапредставлениям сознания? Похоже что здесь они тождественны. ]

** - См. также Квантовые бомбы Элицура-Вайдмана.